Number System in Computer System

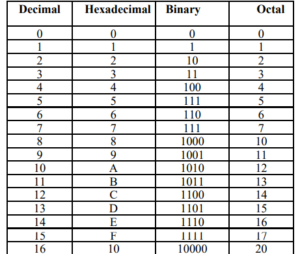
We are familiar with the decimal number system in which digits are 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. The computer uses binary digits for its operation. In the binary system there are only two digits 0 and 1. We will look the other two number systems: Octal Number system and Hexa-decimal Number system.

Let’s see

1. Binary Number System: Given that digital logic and memory devices are based on two electrical states (on and off), it is natural to use a number system, called the binary number system, which contains only two symbols, namely 0 and 1.
2. Decimal Number System: The decimal system is composed of 10 numerals or symbols. These 10 symbols are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9; using these symbols as digitals of a number, we can express any quantity. The decimal system, also called the base- 10 system because it has 10 digits, has evolved naturally as a result of the fact that man has 10 fingers.
3. Octal Number System: Just as the decimal system with its ten digits is a base-ten system, the octal number system with its 8 digits, 0, 1, 2, 3, 4, 5, 6, and 7, is a base-eight system.
4. Hexadecimal Number System: The hexadecimal number system is used as an intermediary system in computers, such as are presentation of memory addresses or a representation of colours. The hexadecimal number system is also known as the base-16 number system, because each position in the number represents an incremental number with a base of 16

Conversion

Numbers expressed in decimal number system are much more meaningful to us, than are numbers expressed in any other number system. This is because we have been using decimal numbers in our day-to- day life, right from childhood; however, we can represent any number in one number system in any other number system. Because the input and final output values are to be in decimal, computer professionals are often required to convert number in other systems to decimal and vice-versa. Many methods can be used to convert numbers from one base to another. A method of converting from another base to decimal, and a method of converting from decimal to another base are described here:

Converting From another Base to Decimal
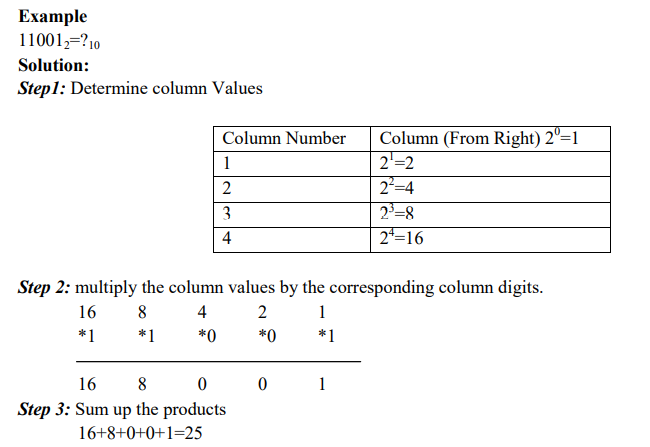
The following steps are used to convert a number in any other base to a base 10 (decimal) number:

1. Determine the column (positional) value of each digit (this depends on the position of the digit and the base of the number system).
2. Multiply the obtained column values (in Step 1) by the digits in the corresponding columns.
3. Sum up the products calculated in Step 2. The total is the equivalent value in decimal.

Converting from Decimal to another Base (Division-Remainder Technique)

The following steps are used to convert a base 10 (decimal) number to a number in another base

1. Divide the decimal number by the value of the new base.
2. Record the remainder from Step 1 as the rightmost digit (least significant digit) of the new base number.
3. Divide the quotient of the previous division by the new base.
4. Record the remainder from Step 3 as the next digit (to the left) of the new base number. Repeat Steps 3 and 4, recording remainders from right to left, until the quotient becomes zero in Step 3. Note that the last remainder, thus obtained, will be the most significant digit of the new base number.